Definición:
Una matriz
es un conjunto de números reales ordenados por filas y columnas.
Uso de las
matrices en la informática:
Las matrices
son utilizadas ampliamente en la informática, por su facilidad y liviandad para
manipular información. También son utilizadas por la informática para resolver
ecuaciones y operaciones algebraicas. En los videos
juegos y sistemas de simulación se emplean muchas veces para representar de
forma abstracta ciertas estructuras de datos que puedan representar algunas
entidades del dominio en estudio. Por ejemplo, se puede representar o concebir
el mapa de un terreno de un juego como una matriz.
Una matriz es un arreglo bidimensional de números (llamados entradas de la matriz) ordenados en filas (o renglones) y columnas, donde una fila es cada una de las líneas horizontales de la matriz y una columna es cada una de las líneas verticales. A una matriz con n filas y m columnas se le denomina matriz n-por-m (escrito 
). El conjunto de las matrices de tamaño se representa como 
, 
es el espacio en donde se introducen los números, siempre entre "[]". El tamaño de una matriz siempre se da con el número de filas primero y el número de columnas después.
Como verán en esta imagen, tenemos una matriz A que posee tres filas y cuatro columnas. 3x4
Siempre se representa el valor de la matriz en orden fila-columna.
En otro caso, si tiene cuatro filas y dos columnas se escribe en la parte inferior de la derecha 4X2. Y así en cualquier caso que se presente.
Dos matrices se dice que son iguales si tienen el mismo tamaño y los mismos elementos en las mismas posiciones.A la entrada de una matriz que se encuentra en la fila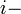
ésima y la columna 
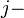ésima se le llama entrada 
o entrada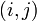 
-ésimo de la matriz. En estas expresiones también se consideran primero las filas y después las columnas
La iésima representa a las filas y la jotaésima a las columnas de una respectiva matriz.
Para nombrar a los elementos de una matriz se siguen los pasos.
). El conjunto de las matrices de tamaño se representa como 
, 
es el espacio en donde se introducen los números, siempre entre "[]". El tamaño de una matriz siempre se da con el número de filas primero y el número de columnas después. Como verán en esta imagen, tenemos una matriz A que posee tres filas y cuatro columnas. 3x4
Siempre se representa el valor de la matriz en orden fila-columna.
En otro caso, si tiene cuatro filas y dos columnas se escribe en la parte inferior de la derecha 4X2. Y así en cualquier caso que se presente.
Dos matrices se dice que son iguales si tienen el mismo tamaño y los mismos elementos en las mismas posiciones.A la entrada de una matriz que se encuentra en la fila
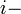ésima y la columna 
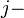ésima se le llama entrada 
o entrada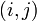 
-ésimo de la matriz. En estas expresiones también se consideran primero las filas y después las columnasLa iésima representa a las filas y la jotaésima a las columnas de una respectiva matriz.
Para nombrar a los elementos de una matriz se siguen los pasos.
A11 sería el elemento de la fila 1 en la columna 1 (se lee A sub uno uno)
A22 sería el elemento de la fila 2 en la columna 2 (se lee A sub dos dos)
A34 sería el elemento de la fila 3 en la columna 4 (se lee A sub tres cuatro)
A32 sería el elemento de la fila 3 en la columna 2 (se lee A sub tres dos)
A23 sería el elemento de la fila 2 en la columna 3 (se lee A sub dos tres)
Todos los elementos se nombran según su posición, si se tiene un elemento en la primera fila y en la cuarta columna se tiene un elemento A14 (A *fila**columna*) aij (i=fila, j=columna)
Tipos de matrices
Matriz fila
Una matriz es aquella que está constituida por una sola fila.
Matriz columna
La matriz columna es aquella que está constituida por una sola columna.
Matriz rectangular
La matriz rectangular tiene distinto número de filas que de columnas, siendo su dimensión mxn.
Matriz traspuesta
Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas.
(At)t = A
(A + B)t = At + Bt
(α ·A)t = α· At
(A · B)t = Bt · At
Matriz nula
En una matriz nula todos los elementos son ceros.
Matriz cuadrada
La matriz cuadrada tiene el mismo número de filas que de columnas. (3X3, 4X4, 5X5)
Los elementos de la forma aii constituyen la diagonal principal.
La diagonal secundaria la forman los elementos con i+j = n+1, siendo n el orden de la matriz.
Tipos de matrices cuadradas
Matriz triangular superior
En una matriz triangular superior los elementos situados por debajo de la diagonal principal son ceros.
Matriz triangular inferior
En una matriz triangular inferior los elementos situados por encima de la diagonal principal son ceros.
Matriz diagonal
En una matriz diagonal todos los elementos que no están situados en la diagonal principal son nulos. La diagonal principal siempre serán los elementos A11, A21, A31.
Matriz escalar
Una matriz escalar es una matriz diagonal en la que los elementos de la diagonal principal son iguales.
Matriz identidad o unidad
Una matriz identidad es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1.
Lo más importante
Comenta: